The World and View Matrix
Andreas Jönsson, March 2002

The world and the view matrix is used to transform vertices that enter the 3D API before they are rendered to the screen. The terms world and view matrix are taken from the DirectX API, but though they may not have the same name in other APIs they will most likely be there in some form. OpenGL for example has a matrix called the model-view matrix. This matrix is a concatenation of DirectX's world and view matrices, thus does the exact same thing although has another name.

In this article I will explain how to use these two matrices to do what you want. I do this because I've noticed that there are many aspiring 3D engine developers that have trouble with this part. I'm going to try to keep this article on a level of generality so that it can be used for any 3D API. I will also try to not go into too much mathematical detail as it really isn't necessary, most APIs do the math for you.

Creating the world matrix

The world matrix is used to transform coordinates from their local coordinate system to the world coordinate system. In other words it transforms the mesh model so that it can be rendered on the right spot in the world. This is useful if you have two (or more) objects in the world that are identical. With the world matrix you don't need to keep duplicate copies of the meshes, instead you just change the world matrix between rendering the two objects.

Normally the world matrix is created by using a few basic transform matrices, such as the translation matrix, rotation matrix, and the scaling matrix. The translation matrix simply moves all the vertices alike, thus translating the object from one point to another without changing its direction or form.

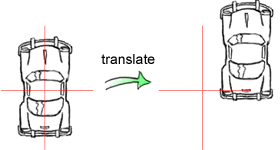
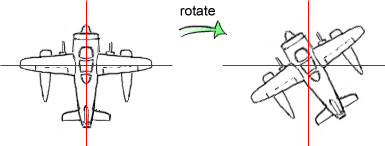
The rotation matrix rotates all vertices around the origin of the coordinate system. You can choose what axis you want to rotate around, the axis doesn't even have to be aligned with one of the 3 major axes, the x, y, or z axis. It's important to remember though that the rotation is always around the origin.

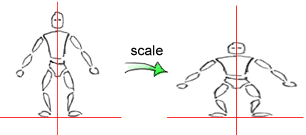
The scaling matrix scales the mesh on the three major axes. This is simply done through multiplication with the scaling factors. Because of the nature of multiplication this is also done around the origin. After all, multiplication with zero always results in zero.

When creating the world matrix the transform matrices are combined into one final matrix by multiplying them with each other. Because of how matrix mathematics works we have to be mindful of the order in which we make the multiplications, else we would get a different result than we really wanted.

Placing a tank in the world

As an example I will show you how to create the world matrix to be used when rendering a tank. To make the example a little more useful I will divide the tank into two models, one for its main body and one for the turret. The turret is able to rotate freely on the tank.

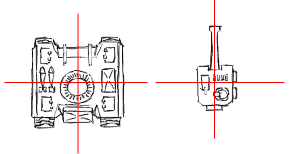
First we need some information about the where the tank is placed in the world and how it's turret is directed. What we have is this:

• Tank position = 10 units north, 5 units east
• Tank direction = 20 degrees to the left
• Turret direction = 30 degrees to the right

We want to render the body of the tank first so we start by computing its world matrix. The first transform to be applied is the rotation since we want to rotate the tank around its origin. The second transform is the translation transform that places the tank on its correct position in the world.

    World_Mtx_Body = Rotation(20)*Translation(10,5)

In my API the vectors are transformed by multiplying with the transform matrix to the right, like this v' = v*M. This means that that the transform matrix that are to the left above will be applied first (in our case the rotation matrix). My hypothetical API just happens to work similarly to DirectX, but for OpenGL you need to reverse the order of the matrices for it to work right.

Now that we have created the world matrix for the body we can go on to create the world matrix for the turret. Again we will start with the rotation matrix since we want to rotate the turret around its origin. Then we will translate the turret because it is situated a little behind the the origin of the body. At this point we have transformed the turret from its local coordinate system into the coordinate system of the tank body, now we need to transform it to its rightful place in the world. Since we already have the matrix for transforming from the coordinate system of the tank body into the world we will use that here too.

    World_Mtx_Turret = Rotation(-30)*Translation(0,-1)*World_Mtx_Body

The turret is transformed by two rotations and two translations, but don't think you can exchange this for one rotation with the sum of the angles and one translation with the sum of the movements, for example like this:

    World_Mtx_Turret_wrong = Rotation(-10)*Translation(10,4)

Using this matrix the turret will have the right direction but it will no longer be placed on top of the tank, which can be a little confusing in games.

Creating the view matrix

The view matrix transforms the world coordinates system into the coordinate system of the camera. In other words, after applying the view matrix transform the coordinates will be relative to the camera and not the origin of the world. If we think of the camera as one of the objects in the world we can see that the view matrix is actually an inverse transform of the camera's world matrix. By inverting the world matrix used to place the camera in the world we get the view matrix.

As you have no doubt heard, inverting a general matrix is a very complicated mathematical process. It is so complicated that I will not even try to explain it. Fortunately there are much simpler ways of creating the view matrix than inverting a world matrix. We will in fact use the same transform matrices mentioned above.

Generally the order of creating a view matrix is by starting with a translation so that the camera position is moved to the origin, followed by a rotation so that the cameras view direction in the world is aligned with the z axis.

Say that we have a camera at position (10,5) and direction 20 degrees left, then we would create the view matrix like the following. Notice how I negate the values to create the inverse of the individual transforms.

    View_Mtx = Translation(-10,-5)*Rotation(-20)

Do you see how this is almost like the world matrix for the tank body? We have in fact inverted the World_Mtx_body matrix that we created above. In general the inversion of a matrix is done by inverting all the individual transforms and then reversing the order, this means that if the individual transforms are known it is quite simple to compute the inversion of the matrix.

Now we can use this knowledge to easily compute the view matrix for a camera placed inside the turret looking through the gun barrel, i.e on the same position and direction as the turret in our example above.

    View_Mtx = Translation(-10,-5)*Rotation(-20)*Translation(0,1)*Rotation(30)

Conclusion

Hopefully I have been able to explain how the world and view matrix is used when rendering a virtual world. If you would like more information into the details about how transform matrices work I suggest you take a course in linear algebra as it will explain all about vectors, matrices, transforms and other stuff done in 3D graphics. Or if you are not on University level yet, you could read the excellent summary on linear algebra that I found on the internet. As always, any question about this article or anything else is welcome.

Further reading

A course in linear algebra, by Ilya Palopezhencev